CRF
CRF
- tag: #NLP #Basis
条件随机场(conditional random field,简称 CRF),是一种鉴别式机率模型,是随机场的一种,常用于标注或分析序列资料,如自然语言文字或是生物序列。
先来张《自然语言处理入门》的图。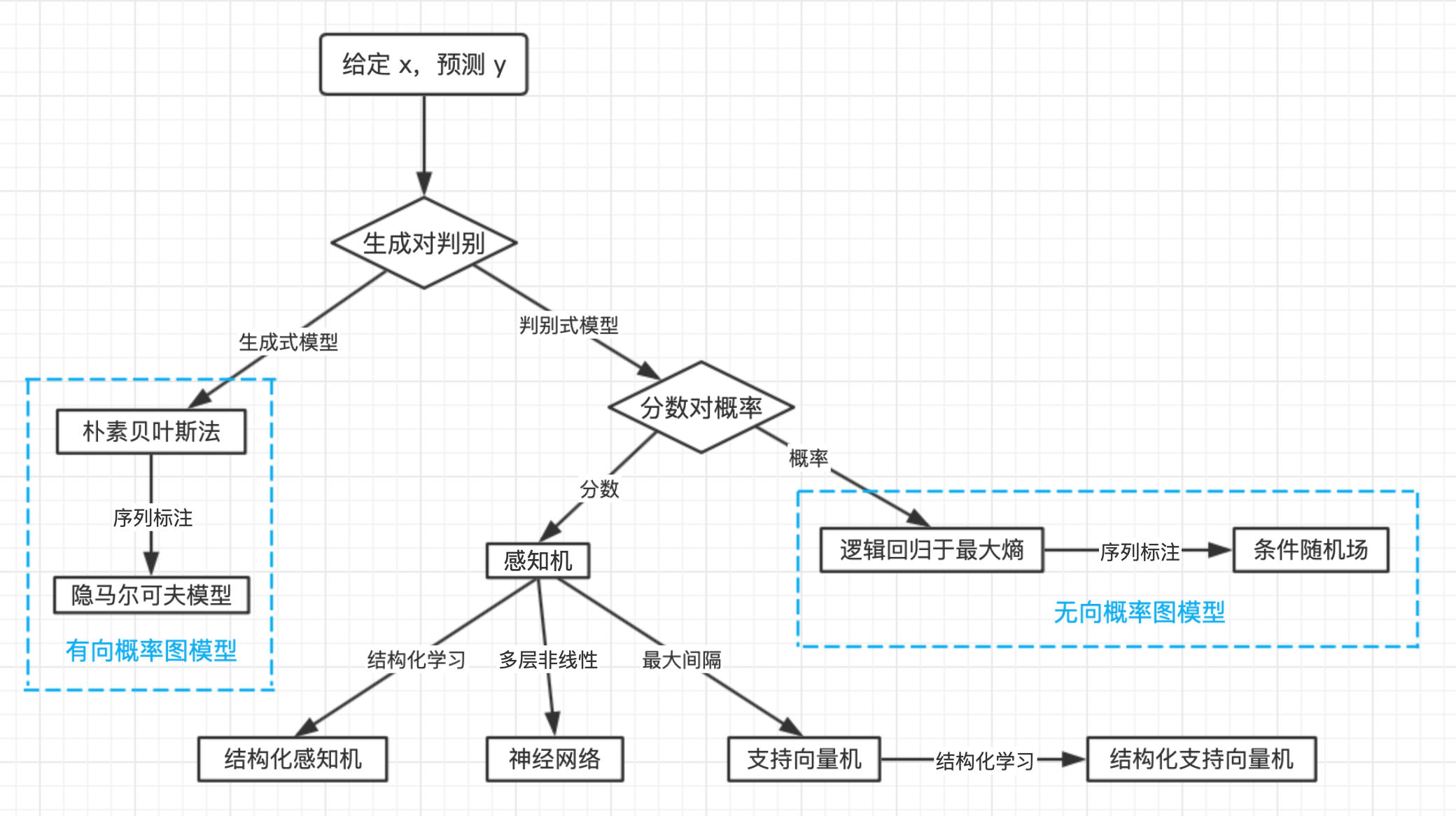
可以浅显地认为,机器学习就是给你随机变量 $x$,求(预测)出另一些随机变量 $y$。
如果 $y$ 是连续型随机变量(如明天的股价),那就是回归问题;如果是离散型随机变量(如这个词的词性),那就是分类问题。
模型
生成式模型
即模拟数据的生成过程,模拟数据的生成过程,两类随机变量存在因果先后关系,先有因素 $y$,后有结果 $x$,这种因果关系由联合分布模拟。
$$p(x,y) = p(y)p(x|y)$$
通过联合分布 $p(x,y)$,生成式模型其实间接建模了 $p(x)$:
$$p(x)=\sum_{y\in{Y}}p(x,y)$$
但由于存在 $p(x)$,导致了两个缺陷:
- $p(x)$ 很难准确估计,因为特征之间并非相互独立,而是存在错综复杂的依赖关系。比如说魑魅魍魉这几个字一般是连在一起的,但隐马尔可夫模型假设它们独立。
- $p(x)$ 在分类中也没有直接作用。
判别式模型
判别式模型跳过了 $p(x)$,直接对条件概率 $p(y|x)$ 建模。不管 $x$ 内部存在多复杂的关系,也不影响判别式模型对 $y$ 的判断,于是就能够利用各种各样有关联的特征。 所以感知机分词的准确率高于隐马尔可夫模型。
$$P(y|x)=\frac{exp(score(x,y))}{\sum_{x,y}exp(score(x,y))}$$
很像 softmax。
概率图
概率图模型(Graphical Model)是用图论方法以表现数个独立随机变量之关联的一种建模方法。一个 $p$ 个节点的图中,节点 $i$ 对应一个随机变量,记为 $X_{i}$ 。
它利用节点 $V$ 来表示随机变量,用边 $E$ 连接有关联的随机变量,将多维随机变量分布$p(x,y)$表示为图 $G=(V,E)$。
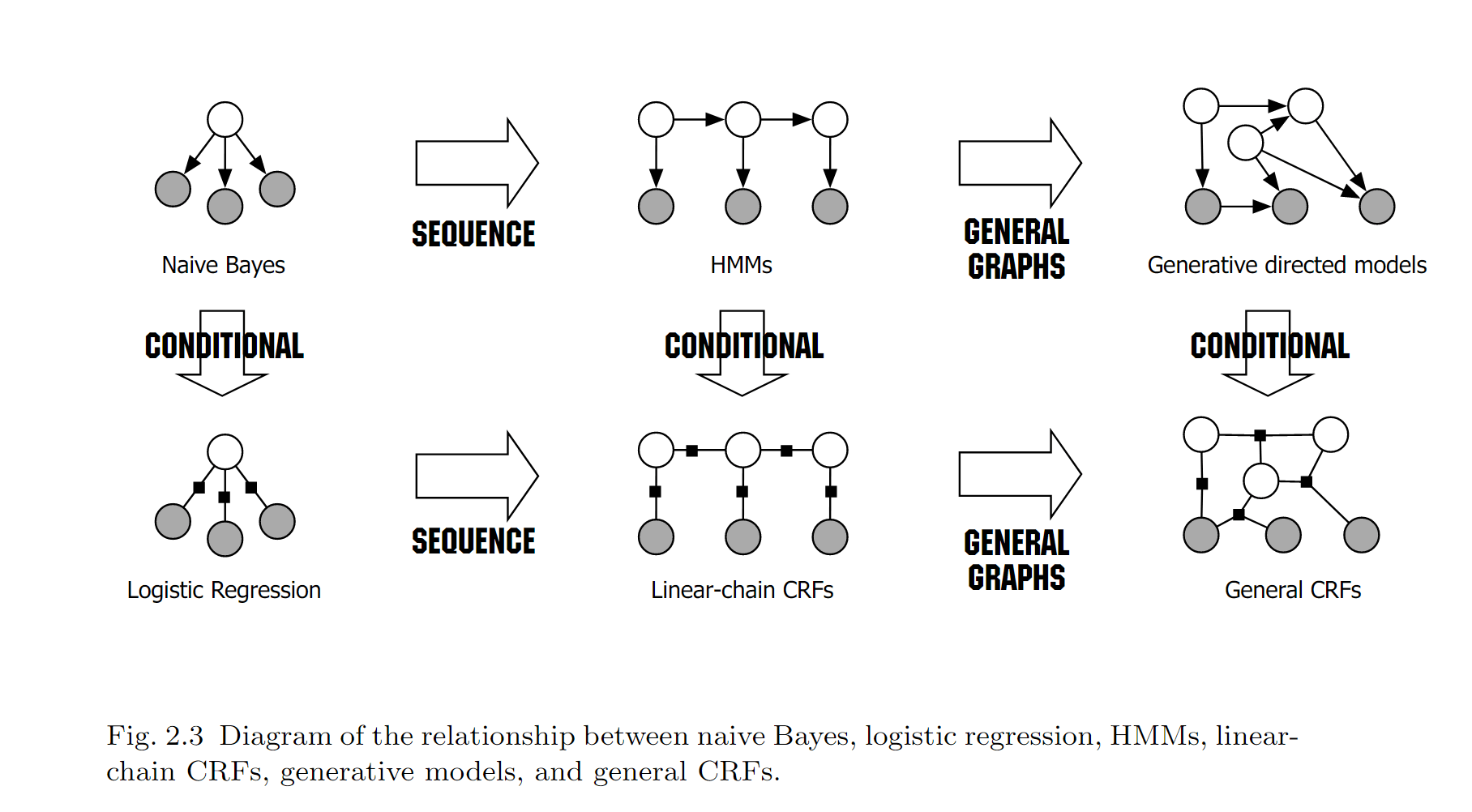
有向概率图模型
按事件的先后因果顺序将节点连接为有向图。如果事件 A 导致事件 B,则用箭头连接两个事件 A–>B。
有向图模型都将概率有向图分解为一系列条件概率之积,有向图模型经常用生成式模型来实现。定义 $\pi(v)$ 表示节点 $v$ 的所有前驱节点,则分布为:
$$p(\boldsymbol{x}, \boldsymbol{y})=\prod_{v=V} p(v | \boldsymbol{\pi}(v))$$
无向概率图模型
无向图模型则不探究每个事件的因果关系,也就是说不涉及条件概率分解。无向图模型的边没有方向,仅仅代表两个事件有关联。
无向图模型将概率分解为所有最大团上的某种函数之积。在图论中,最大团指的是满足所有节点相互连接的最大子图。因为最大团需要考虑所有变量,为此,无向图模型定义了一些虚拟的因子节点,每个因子节点只连接部分节点,组成更小的最大团。
无向图模型将多维随机变量的联合分布分解为一系列最大团中的因子之积:
$$p(x, y)=\frac{1}{Z} \prod_{a} \Psi_{a}\left(x_{a}, y_{a}\right)$$
其中,$a$ 是因子节点,$\Psi_{a}$ 则是一个因子节点对应的函数,参数 $x_{a}, y_{a}$ 是与因子节点相连的所有变量节点。为了将上述式子约束为概率分布,定义常数 $Z$ 为如下归一化因子:
$$Z=\sum_{x, y} \prod_{a} \Psi_{a}\left(x_{a}, y_{a}\right)$$
在机器学习中,常用指数家族的因子函数:
$$\Psi_{a}\left(x_{a}, y_{a}\right)=\exp \left\{\sum_{k} w_{a k} f_{a k}\left(x_{a}, y_{a}\right)\right\}$$
其中,$k$ 为特征的编号,$f_{ak}$ 是特征函数,$w_{ak}$ 为相应的特征权重。
判别式模型经常用无向图来表示,只需要在归一化时,对每种 $x$ 都求一个归一化因子:
$$Z(\boldsymbol{x})=\sum_{y} \prod_{a} \Psi_{a}\left(\boldsymbol{x}_{a}, \boldsymbol{y}_{a}\right)$$
然后 P(x,y) 就转化为判别式模型所需的条件概率分布,也是条件随机场的一般形式:
$$p(\boldsymbol{y} \mid \boldsymbol{x})=\frac{1}{Z(\boldsymbol{x})} \prod_{a} \boldsymbol{\Psi}_{a}\left(\boldsymbol{x}_{a}, \boldsymbol{y}_{a}\right)$$
随机场
随机场是由若干个位置组成的整体,当给每一个位置中按照某种分布随机赋予一个值之后,其全体就叫做随机场。
举词性标注的例子:假如有一个个词形成的句子需要做词性标注。这十个词每个词的词性可以在已知的词性集合(名词,动词等)中去选择。当我们为每个词选择完词性后,这就形成了一个随机场。
马尔可夫随机场
马尔可夫属性是指随机过程的无记忆属性。通俗来说,它指的是一个随机变量序列按时间先后关系依次排开的时候,第 N+1 时刻的分布特性,只跟 N 时刻的随机变量的取值有关,与 N 时刻以前的随机变量的取值无关(当然,这里只是指一阶马尔可夫性质,如果是 k 阶马尔可夫,那么就是跟前面 K 个时刻的随机变量的取值相关)。
举词性标注的例子:如果我们假设所有词的词性只和它相邻的词的词性有关时,这个随机场就特化成一个马尔科夫随机场。比如第 $n$ 个词的词性除了与自己本身的位置有关外,只与第 $n-1$ 个词和第 $n+1$ 个词的词性有关。
条件随机场
CRF 是马尔科夫随机场的特例,它假设马尔科夫随机场中只有 X 和 Y 两种变量,X 一般是给定的,而 Y 一般是在给定 X 的条件下的输出。
设$X$与$Y$是随机变量,$P(Y|X)$是给定时的条件概率分布,若随机变量 $Y$ 构成的是一个马尔科夫随机场,则称条件概率分布 $P(Y|X)$ 是条件随机场。
举词性标注的例子:$X$ 是词,$Y$ 是词性,如果我们假设它是一个马尔科夫随机场,那么它也就是一个 CRF。
线性条件随机场(Linear-CRF)
注意在 CRF 的定义中,我们并没有要求 $X$ 和 $Y$ 有相同的结构。当它们结构相同时,即 $X=(x_1,x_2,…,x_T),Y=(y_1,y_2,…,y_T)$,均为线性表示的随机变量序列,在给定随机变量序列$X$的情况下,随机变量$Y$的条件概率分布$P(Y|X)$构成条件随机场,即满足马尔科夫性质$P(y_t|X,y_1,y_2,…,y_T)=P(y_t|X,y_{t-1},y_{t+1})$,这就构成了线性链条件随机场。
定义如下:
$$p(\boldsymbol{y} \mid \boldsymbol{x})=\frac{1}{Z(\boldsymbol{x})} \prod_{t=1}^{T} \exp \left\{\sum_{k=1}^{K} \boldsymbol{w}_{k} f_{k}\left(y_{t-1}, y_{t}, \boldsymbol{x}_{t}\right)\right\}$$
其中,$Z(x)$为归一化函数:
$$Z(\boldsymbol{x})=\sum_{y} \prod_{t=1}^{T} \exp \left\{\sum_{k=1}^{K} w_{k} f_{k}\left(y_{t-1}, y_{t}, \boldsymbol{x}_{t}\right)\right\}$$
上式定义在所有可能的标注序列上。如果将所有特征函数与权重分别写作向量形式$\phi(y_{t-1},y_t,\boldsymbol{w}_t),\boldsymbol{w} \in \mathbb{R}^{K\times1}$,则线性链条件随机场的定义可简化为:
$$\begin{aligned}
p(\boldsymbol{y} \mid \boldsymbol{x}) &=\frac{1}{Z(\boldsymbol{x})} \prod_{t=1}^{T} \exp \left{\boldsymbol{w} \cdot \phi\left(y_{t-1}, y_{t}, \boldsymbol{x}_{t}\right)\right} \
&=\frac{1}{Z(\boldsymbol{x})} \exp \left{\sum_{t=1}^{T} \boldsymbol{w} \cdot \phi\left(y_{t-1}, y_{t}, \boldsymbol{x}_{t}\right)\right}
\end{aligned}$$